Nous avons notre objectif : trouver les paramètres a et b qui minimisent la fonction de coût MSE. La question est : comment ?

Imagine que tu es Inoxtag en pleine descente de l’Everest. Soudain, une tempête de neige se lève, le brouillard est total et ta visibilité est réduite à quelques pas. Ton objectif est vital : atteindre le camp de base situé au point le plus bas le plus vite possible pour te mettre en sécurité. Tu n’as aucune visibilité sur la vallée, mais à tes côtés se trouve ton sherpa, Manish. À chaque instant, il analyse la pente juste autour de vous. Il est ton guide, ton gradient. Il t’indique la direction de la descente la plus sûre et la plus efficace. Tu lui fais confiance et tu fais un pas prudent dans cette direction. Vous répétez ce processus, pas après pas, descendant la montagne jusqu’à atteindre enfin la sécurité du camp.

Eh bien, la descente de gradient est exactement ça ! C’est un algorithme d’optimisation qui “descend” la fonction de coût pour en trouver le minimum.

• La montagne : c’est notre fonction de coût (la courbe en forme de bol que l’on a vue).
• Ta position (latitude/longitude) : ce sont les valeurs actuelles de nos paramètres $a$ et $b$.
• L’altitude : c’est la valeur de l’erreur MSE pour les $a$ et $b$ actuels.
• Le point le plus bas de la vallée : c’est le MSE minimum, correspondant aux meilleures valeurs possibles pour $a$ et $b$.

Le Gradient : la boussole qui indique la pente

Pour savoir dans quelle direction faire un pas, l’algorithme a besoin de “sentir la pente”. En mathématiques, l’outil qui nous donne la direction et l’intensité de la pente la plus raide s’appelle le gradient.

Le gradient est comme un sherpa : il pointe toujours vers le haut de la montagne. Mais nous, on veut descendre ! Donc, c’est très simple : on calcule le gradient, et on fait un pas dans la direction opposée.

À chaque étape, l’algorithme va :

1. Calculer le gradient de la fonction de coût pour les valeurs actuelles de $a$ et $b$.
2. Mettre à jour $a$ et $b$ en faisant un petit pas dans la direction opposée au gradient.

[Image du graphique en forme de bol avec des flèches montrant la descente par étapes successives vers le point le plus bas]

La formule théorique de mise à jour

D’un point de vue plus mathématique, la mise à jour des paramètres à chaque étape est définie par la formule suivante :

Où :

• := signifie qu’on affecte la nouvelle valeur au paramètre.
• $\alpha$ (alpha) est le taux d’apprentissage (learning rate). C’est lui qui contrôle la taille du pas, on détaille ça juste en dessous.
• gradient_du_paramètre est le résultat du calcul de la dérivée partielle que nous venons de voir.

Cette simple formule est appliquée simultanément à $a$ et à $b$ à chaque itération.

Le calcul du gradient (la partie un peu mathématique)

Tu te demandes sûrement : “D’accord, mais comment la machine calcule-t-elle cette fameuse pente ?” ce gradient_du_paramètre. C’est là qu’intervient un outil mathématique puissant : la dérivée.

Sans entrer dans un cours de mathématiques complet, retiens simplement ceci : la dérivée d’une fonction en un point nous donne la pente de cette fonction à cet endroit précis. Comme notre fonction de coût (la MSE) dépend de deux paramètres ($a$ et $b$), nous allons utiliser des dérivées partielles pour calculer la pente selon $a$ et la pente selon $b$ indépendamment. Si tu veux une remise à niveau ou découvrir les notions de dérivée et dérivées partielles, tu peux consulter les modules suivants :

La fonction de coût MSE est : $MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$

Les formules pour obtenir le gradient sont issues de la dérivation de cette fonction. Le résultat de ce calcul nous donne :

• Pour le paramètre “ (l’inclinaison de la droite) : $gradient\_de\_a = \frac{\partial MSE}{\partial a} = \frac{2}{n} \sum_{i=1}^{n} -x_i \times (y_i - \hat{y}_i)$
• Pour le paramètre “ (l’ordonnée à l’origine) : $gradient\_de\_b = \frac{\partial MSE}{\partial b} = \frac{2}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)$

Si tu souhaites approfondir la démonstration des formules ci-dessus, relatives aux dérivées partielles, tu peux consulter le module suivant :

Ces deux formules sont au cœur du calcul. Elles permettent à l’algorithme de savoir précisément de combien et dans quelle direction il doit ajuster $a$ et $b$ pour faire diminuer l’erreur.

Le Taux d’Apprentissage (Learning Rate) : la taille de nos pas

Une question cruciale se pose : quelle doit être la taille de nos pas ? Ce paramètre, $\alpha$, est l’un des plus importants en IA.

• Si le taux d’apprentissage est trop petit : On fait de tout petits pas. C’est prudent, on est sûr de ne pas manquer le fond de la vallée. Mais cela peut prendre un temps infini pour y arriver ! L’apprentissage sera très, très lent.
• Si le taux d’apprentissage est trop grand : On fait des pas de géant. On risque de “sauter” par-dessus le fond de la vallée et de se retrouver de l’autre côté, parfois même plus haut qu’au départ ! Le modèle n’arrivera jamais à trouver le minimum et son erreur pourrait même augmenter. On dit que l’algorithme diverge.

[Image comparative montrant trois chemins de descente : un avec un learning rate trop petit (beaucoup de petits pas), un trop grand (qui rebondit et s’éloigne), et un optimal (qui converge rapidement)]

Trouver un bon taux d’apprentissage est donc un art subtil. C’est un équilibre entre la vitesse d’apprentissage et la précision.

🙌 À la mano : un pas de descente

Pour que tout soit bien clair, suivons l’algorithme pour une seule étape.

Imaginons que nous n’avons que deux singes dans nos données pour illustrer le calcul ($n=2$).

Supposons que notre algorithme démarre avec les paramètres (choisis un peu au hasard) :

• $a = 0.5$
• $b = 1$
• Taux d’apprentissage $\alpha = 5e-5$

Étape 1 : Faire les prédictions Avec les $a$ et $b$ actuels, quel poids le modèle prédit-il pour chaque singe ?

• Prédiction Singe 1 : $\hat{y}_1 = a \times x_1 + b = 0.5 \times 60 + 1 = 31 kg$
• Prédiction Singe 2 : $\hat{y}_2 = a \times x_2 + b = 0.5 \times 80 + 1 = 41 kg$

On voit que nos prédictions (31 et 41 kg) sont au dessus des poids réels (8 et 11 kg).

Étape 2 : Calculer le gradient On applique les formules vues plus haut en faisant la somme (Σ) pour nos deux singes.

• Calcul du gradient_de_a : $gradient\_de\_a = \frac{\partial MSE}{\partial a} = \frac{2}{n} \sum_{i=1}^{n} -x_i \times (y_i - \hat{y}_i)$

• Terme pour Singe 1 : $-x_1 \times (y_1 - \hat{y}_1) = -60 \times (8 - 31) = 1380$

• Terme pour Singe 2 : $-x_1 \times (y_1 - \hat{y}_1) = -80 \times (11 - 41) = 2400$

• Somme $\sum = 1380+ 2400 = 3780$

• $gradient\_de\_a = \frac{2}{2} \times 3780 = 3780$

• Calcul du gradient_de_b : $gradient\_de\_b = \frac{\partial MSE}{\partial b} = \frac{2}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)$

• Terme pour Singe 1 : $y_1 - \hat{y}_1 = 8 - 31 = -23$

• Terme pour Singe 2 : $y_2 - \hat{y}_2 = 11 - 41 = -30$

• Somme $\sum = -23 + (-30) = -53$

• $gradient\_de\_b = \frac{2}{2} \times -53 = -53$

Étape 3 : Mettre à jour les paramètres On applique la formule $nouveau\_paramètre := paramètre\_actuel - α \times (gradient\_du\_paramètre)$

• Nouveau $a = 0.5 - (5e-5 \times 3780) = 0.5 - 0.189 = 0.311$
• Nouveau $b = 1 - (5e-5 \times -53) = 1 - (-0.00265) = 1.00265$

Conclusion de l’étape : Après une seule itération, nos nouveaux paramètres sont $a = 0.311$ et $b = 1.00265$. Le modèle a appris de ses erreurs et a ajusté sa droite pour qu’elle corresponde un peu mieux aux données. Il répétera ce processus des milliers de fois pour affiner ces valeurs jusqu’à trouver les meilleures possibles. On peut d’ailleurs utiliser ces nouvelles valeurs pour vérifier que la nouvelle prédiction s’améliore.

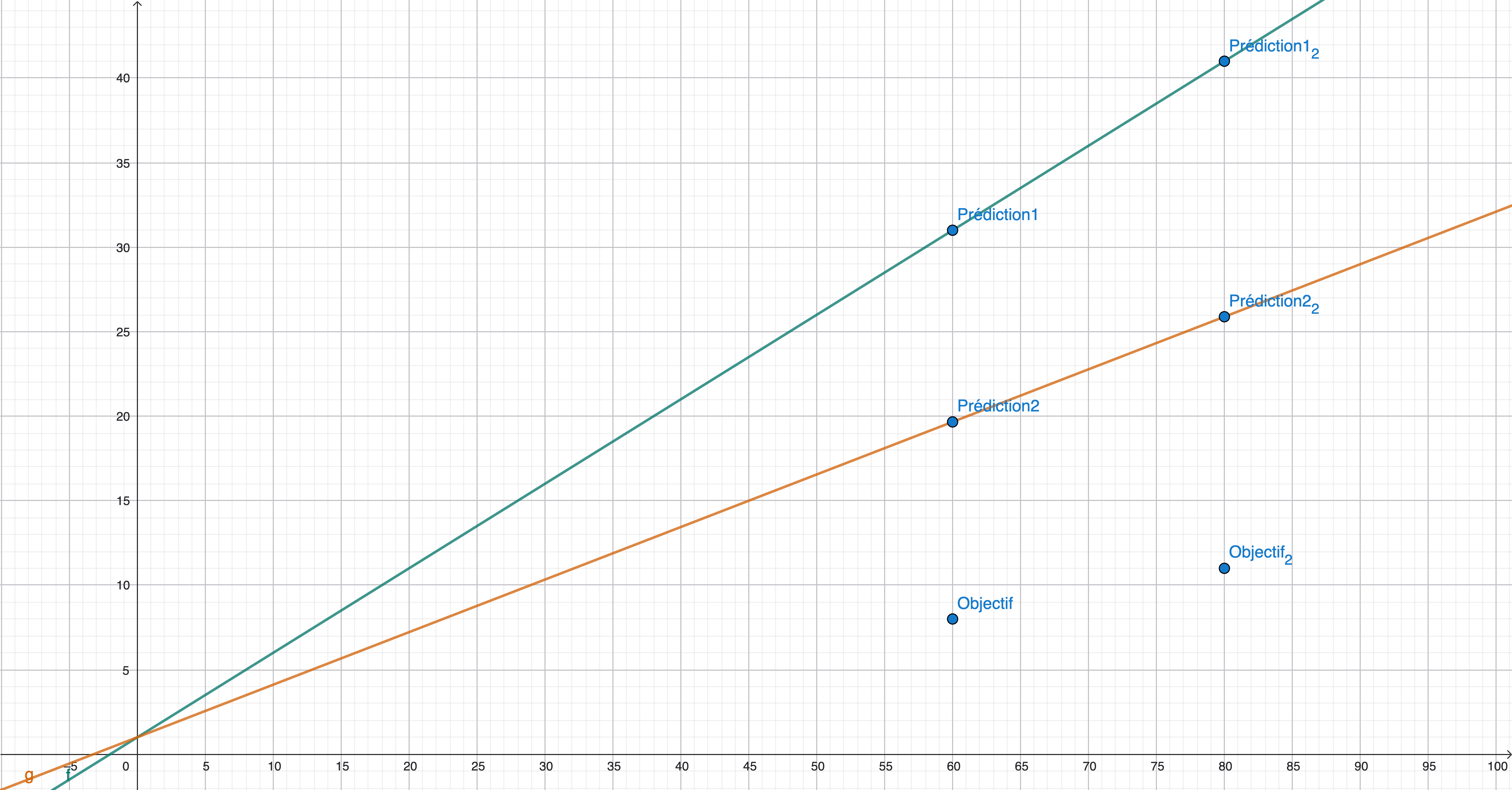
Le graphique ci-dessous illustre la modification des paramètres et l’avolution de la courbe. Nous constatons que la prédiction 2 se rapproche ainsi de l’objectif souhaité.

Le processus d’entraînement de notre régression linéaire avec la descente de gradient se résume donc à ceci :

1. Initialisation : Choisir des valeurs de départ aléatoires pour a et b.

2. Répéter (pendant un certain nombre d’itérations, appelées epochs) :

3. a. Calculer le gradient de la MSE par rapport à $a$ et $b$.

4. b. Mettre à jour a et b avec la formule.

5. Fin : Au bout de nombreuses itérations, a et b convergeront vers les valeurs optimales qui minimisent la MSE.

Et voilà ! Tu as compris le mécanisme fondamental qui permet aux modèles d’apprendre de leurs erreurs. C’est ce même principe, bien que complexifié, qui est au cœur des réseaux de neurones les plus avancés.