La fameuse régression linéaire
Comme vu dans le chapitre précédent (Que veut dire le mot “Régression”), la régression linéaire est notre premier outil pour modéliser la relation entre une variable d’entrée et une variable de sortie à l’aide d’une ligne droite. L’exemple que nous avons pris était la relation entre la taille d’un singe et sa masse, qui peut être traduit par une droite comme illustré dans le graphique ci-dessous :
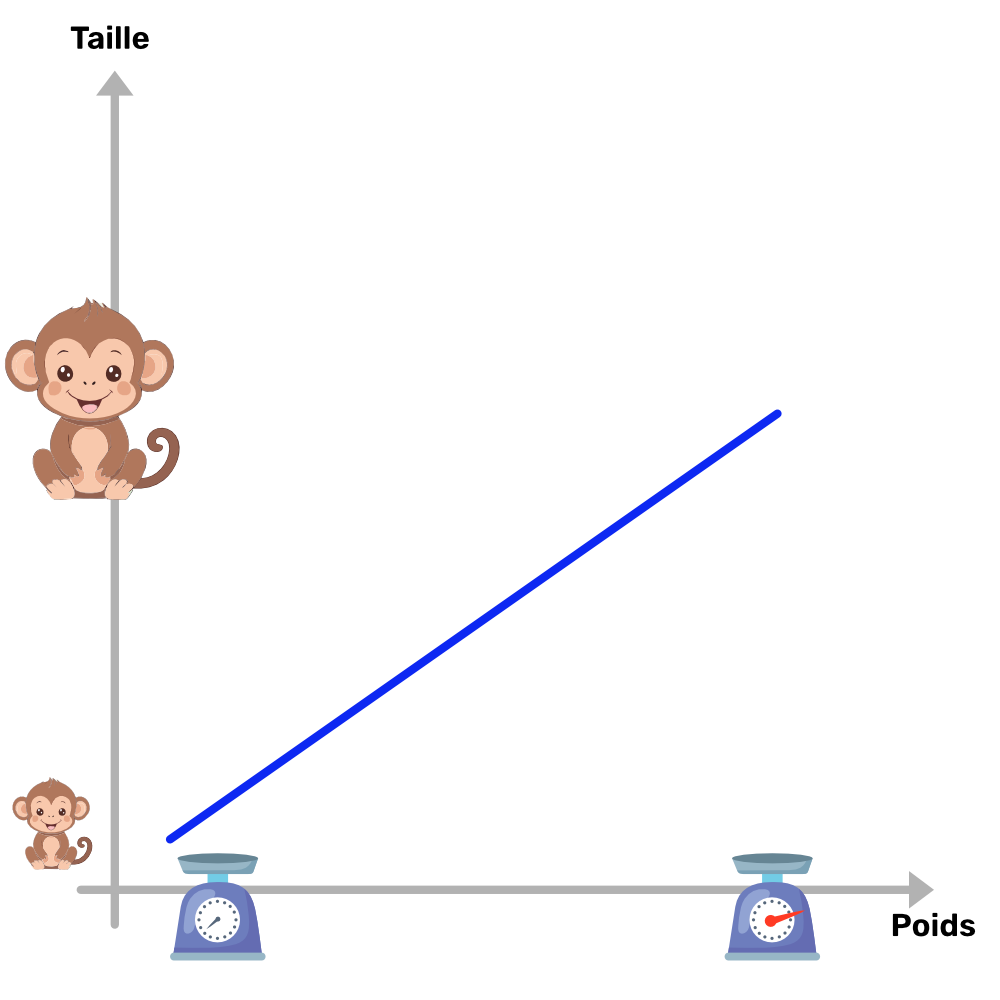
Plus le singe va être grand, plus celui-ci va avoir un poids (une masse) élévé. Tous l’objectif de la regression linéaire et de construire cette droite via des données observées. En tant que zoologiste, tu as relevé la taille et le poids de plusieurs individus. Tes données ressemblent à quelque chose comme ça :
| Taille (cm) | Poids (kg) |
|---|---|
| 50 | 30 |
| 100 | 60 |
| 180 | 80 |
| 120 | 75 |
| … | … |
Tout l’objectif est maintenant d’extrapoler la meilleure droite permettant de représenter la relation entre la taille et le poids.
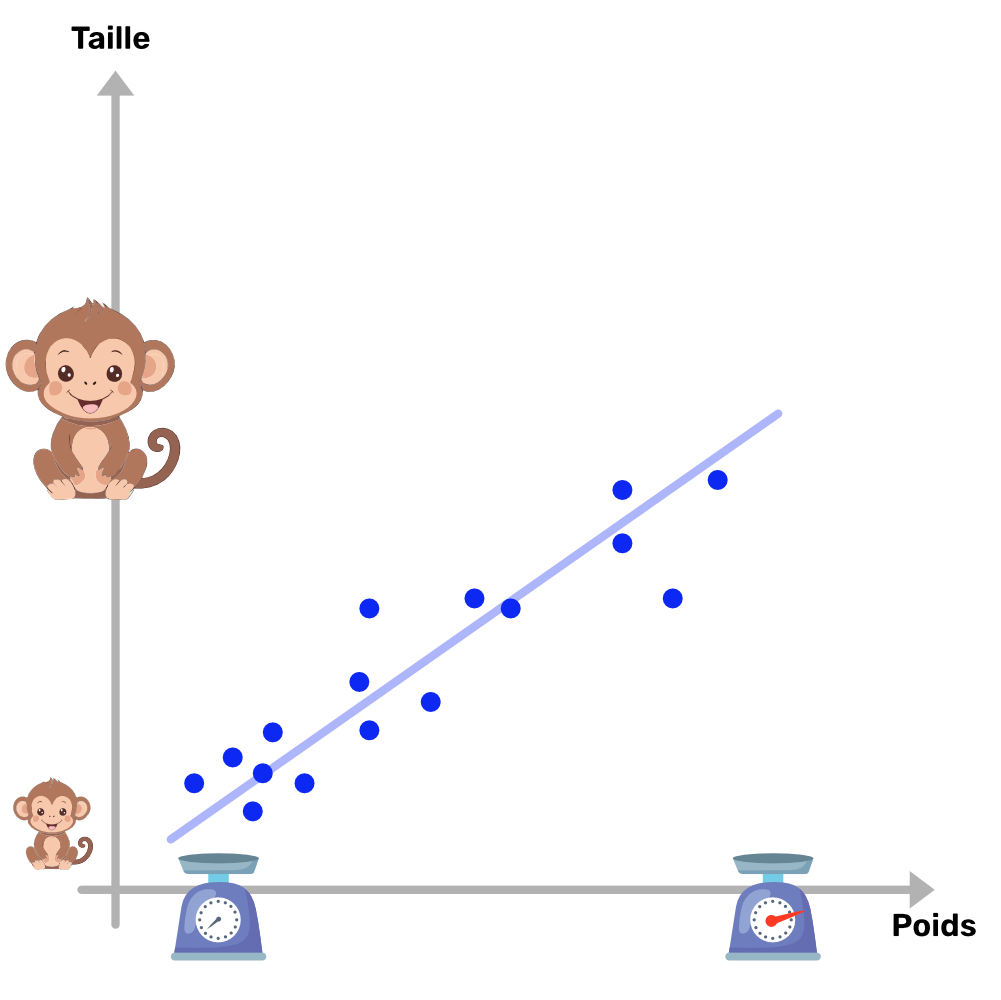
Une droite, c’est une équation mathématique très simple : . Dans notre cas, cela se traduit par :
x(la taille) est notre entrée.y(le poids) est la sortie que l’on veut prédire.aetbsont les paramètres du modèle.areprésente la pente de la droite (à quel point le poids augmente quand la taille augmente) etbest l’ordonnée à l’origine (une valeur de base).
“Apprendre” ou “entraîner” notre modèle de régression linéaire, c’est tout simplement trouver les valeurs parfaites de a et b.
La “meilleure” droite est celle qui minimise l’erreur globale. Pour chaque singe de tes données, l’erreur est la distance verticale entre son poids réel (le point) et le poids prédit par la droite. L’algorithme va donc tester plein de droites différentes (en ajustant a et b) jusqu’à trouver celle pour qui la somme de toutes ces erreurs est la plus petite possible.

Une fois que le modèle a trouvé les meilleures valeurs pour a et b, c’est gagné ! Tu as un modèle entraîné. Tu peux maintenant prendre la taille de n’importe quel nouveau singe, l’injecter dans la formule, et obtenir une prédiction fiable de son poids. Pratique, non ?
Mais attends une minute… comment l’algorithme sait-il ce qu’est “la plus petite erreur possible” ou encore “la meilleure droite” ? Pour pouvoir minimiser quelque chose, il faut d’abord être capable de le mesurer ! C’est là qu’intervient un concept absolument central en intelligence artificielle : la Fonction de Coût (ou Cost Function). Elle nous donne une note qui évalue à quel point notre modèle se trompe.
Dans le prochain chapitre, nous allons découvrir la fonction de coût la plus utilisée pour la régression linéaire : l’Erreur Quadratique Moyenne (ou Mean Squared Error - MSE). Tu verras, c’est l’outil qui va guider notre modèle pour qu’il devienne le meilleur possible.