Fonction de coup : Erreur Quadratique Moyenne (MSE)
Comme on l’a vu à la fin du chapitre précédent, pour trouver la “meilleure” droite, notre algorithme a besoin d’un moyen de noter ses propres performances. Il lui faut un juge impartial qui lui dit : “Là, ta prédiction est bonne” ou “Ouh là, tu es très loin de la vérité !”. Ce juge, c’est la fonction de coût.
Son rôle est de calculer un score d’erreur unique qui résume la performance du modèle sur l’ensemble des données. Plus le score est bas, meilleur est le modèle.
Loss Function vs. Cost Function : une petite subtilité
Avant d’aller plus loin, il est utile de connaître une petite distinction de vocabulaire que tu rencontreras souvent. Même si les termes sont parfois utilisés de manière interchangeable, il y a une nuance :
- La Loss Function (Fonction de Perte) : Elle mesure l’erreur pour un seul exemple de tes données. Par exemple, pour un seul de nos singes, on calcule l’écart entre son poids réel et le poids que notre droite a prédit. C’est une mesure d’erreur locale.
- La Cost Function (Fonction de Coût) : C’est la moyenne des erreurs sur l’ensemble de tes données. On calcule l’erreur pour chaque singe, puis on fait la moyenne de tout ça pour avoir une vision globale de la performance du modèle. C’est ce score global que l’on va chercher à minimiser.
En résumé : la Loss c’est l’erreur sur un point, la Cost c’est l’erreur moyenne sur tous les points.
L’Erreur Quadratique Moyenne (MSE) à la loupe
Pour la régression linéaire, la fonction de coût la plus populaire est de loin l’Erreur Quadratique Moyenne (ou Mean Squared Error en anglais, d’où l’acronyme MSE). Ne te laisse pas intimider par le nom, on va le décortiquer ensemble, c’est très simple !
Reprenons nos singes. Pour calculer la MSE, on suit 3 étapes :
-
Calculer l’erreur pour chaque singe : Pour chaque singe, on calcule la différence entre son poids réel et le poids prédit par notre modèle. C’est la distance verticale dont on parlait au chapitre 2.
-
Mettre cette erreur au carré (Quadratique) : On prend chaque erreur calculée et on la multiplie par elle-même. Pourquoi faire ça ? Pour deux raisons très malignes :
- Éliminer les négatifs : Si le modèle prédit un poids plus lourd, l’erreur est négative (ex: ). S’il prédit plus léger, elle est positive (ex: ). En mettant au carré, on ne garde que l’amplitude de l’erreur. Une erreur de est aussi “mauvaise” qu’une erreur de .

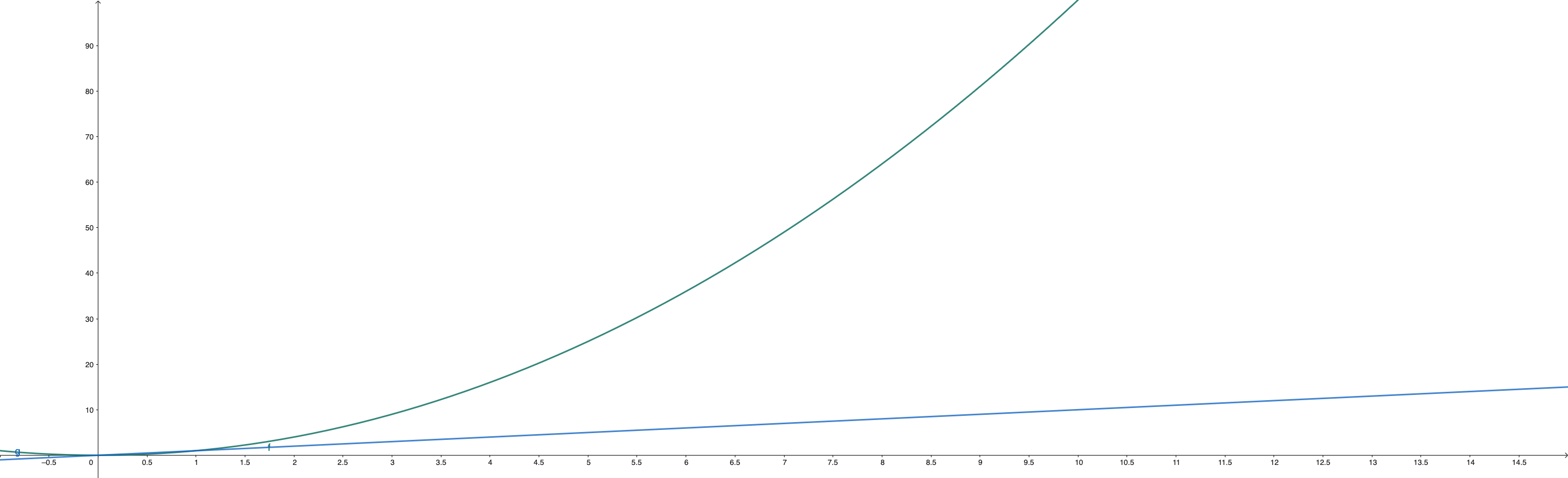
- Pénaliser les grosses erreurs : Mettre au carré a un effet amplificateur. Une petite erreur de 2 deviendra 4. Mais une grosse erreur de 100 deviendra 10 000 ! Cela force le modèle à se concentrer en priorité sur la correction de ses prédictions les plus mauvaises. La figure ci-dessous montre l’évolution de la fonction quadratique comparée à une fonction linéaire :
- Éliminer les négatifs : Si le modèle prédit un poids plus lourd, l’erreur est négative (ex: ). S’il prédit plus léger, elle est positive (ex: ). En mettant au carré, on ne garde que l’amplitude de l’erreur. Une erreur de est aussi “mauvaise” qu’une erreur de .
-
Faire la moyenne (Moyenne) : On additionne toutes les erreurs au carré que l’on vient de calculer, et on divise par le nombre total de singes. On obtient alors un seul chiffre : la MSE. C’est le score final de notre modèle.
La formule mathématique qui résume tout ça est la suivante :
Où :
nest le nombre total de singes dans notre jeu de données.- est la valeur réelle pour le singe
i(son vrai poids). - (prononcé “y chapeau”) est la valeur prédite par le modèle pour le singe
i.
🙌 À la mano : un exemple concret
Pour être sûr que tu as bien compris, faisons un calcul ensemble, à la main ! Imaginons que nous avons 3 singes et que notre modèle (notre droite y = ax + b avec des valeurs de a et b pour l’instant choisies au hasard) a fait les prédictions suivantes :
| Singe | Poids Réel (y) | Poids Prédit (ŷ) |
|---|---|---|
| 1 | 30 kg | 39 kg |
| 2 | 67 kg | 87 kg |
| 3 | 98 kg | 80 kg |
Déroulons les 3 étapes du calcul de la MSE :
- Calculer l’erreur pour chaque singe :
- Singe 1 :
- Singe 2 :
- Singe 3 :
- Mettre chaque erreur au carré :
- Singe 1 :
- Singe 2 :
- Singe 3 :
- Faire la moyenne de ces valeurs :
- Somme des erreurs au carré :
- Moyenne (on divise par le nombre de singes, ici 3) :
Le score MSE de notre modèle actuel est donc de 268,3. Ce chiffre, à lui seul, représente la performance globale de notre droite. Le but du jeu sera d’ajuster a et b pour que ce score soit le plus bas possible.
Voilà ! Notre objectif est maintenant limpide : trouver les valeurs de a et b (la pente et l’ordonnée de notre droite) qui rendent ce score MSE le plus petit possible. Mais comment faire pour trouver ces valeurs magiques sans tester toutes les droites de l’univers ? C’est ce que nous verrons dans le prochain chapitre en parlant d’un algorithme appelé la “Descente de Gradient”.